Como decíamos en un artículo anterior, una de las aplicaciones de la Estadística (y la Computación) de más interés en la actualidad en el ámbito de la Seguridad, es la que trata del al análisis y gestión de tiempos de evacuación.
En efecto, los recientes acontecimientos referidos a acciones terroristas contra peatones en vías con gran afluencia de personas (o locales que albergan grandes masas de gente), plantean la necesidad de realizar estudios de prevención (o previos al evento) que no solo se refieran a la definición de las salidas o vías de evacuación, que deben expresarse en el preceptivo Plan de Emergencia, sino también al tiempo que se necesita para una completa evacuación de la zona o local. El interés en obtener un cálculo del tiempo, diremos probable, de evacuación tiene obviamente interés en sí mismo, porque los efectos del suceso que se trate pueden empeorar con el tiempo, como por ejemplo lo es en caso de incendio.
Hasta muy recientemente no ha sido posible realizar el cálculo de estos tiempos de evacuación, por medio de escenarios en los que pudiera simularse la dinámica del comportamiento de las personas. De hecho, todavía en la actualidad, la inmensa mayoría de los Planes de Emergencia o de Autoprotección se basan en meras tablas de tiempos en función del tipo de recinto, o en los tiempos calculados por medio de simulacros periódicos. No obstante, estos simulacros no suelen plantear cambios en el escenario, como salidas canceladas o impracticables, ni evidentemente sobre las mejoras que puedan realizarse sobre el mismo, entre otras cosas porque pueden estar planificadas pero no ejecutadas, o simplemente intuidas. Un ejemplo muy clarificador puede ser el plantear qué nueva medida puede mejorar la evacuación de un local: si la apertura de una nueva salida, el ensanche de una salida existente, la instalación de una escalera de incendios, etc.
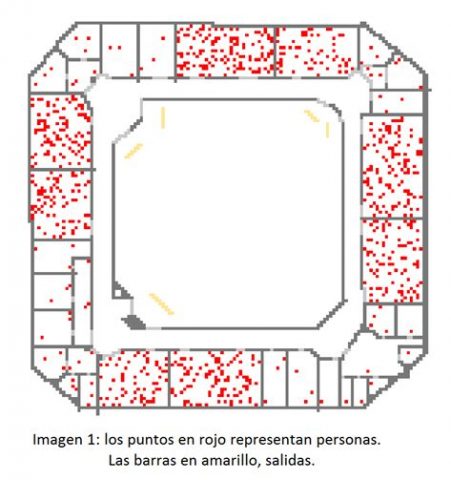
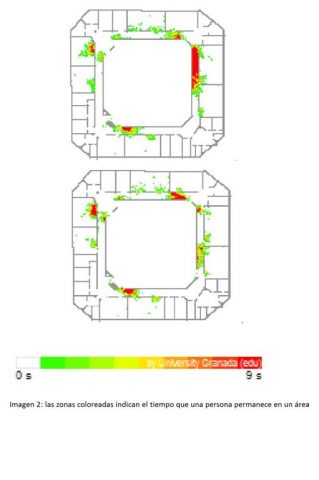
En la Facultad de Ciencias del Trabajo de la Universidad de Granada nos hemos planteado esta cuestión, y con ayuda del software PedGo (http://www.traffgo-ht.com/en/index.html) hemos realizado una simulación en la que hemos obtenido los tiempos de evacuación de la primera planta del edificio que ocupa la Facultad. El planteamiento ha consistido en calcular el tiempo de evacuación para la planta simulada del edificio (obsérvese la imagen 1) y su comprobación a la adecuación sobre el tiempo «real» obtenido en un simulacro, a modo de calibración. Una vez calibrada la simulación, procedimos a realizar una nueva simulación en el supuesto de la instalación de una escalera de incendios. La imagen 2 muestra las zonas, en rojo, con mayor densidad de personas y el tiempo que permanecen en esa zona, para el caso actual (izquierda) y el caso en el que se incorpora una escalera de incendios (derecha). Los resultados de ese cambio de condiciones muestran claramente que la incorporación de dicha escalera atenúa el número de zonas con apelotonamientos, con una disminución adicional del tiempo en dichos apelotonamientos. Es fácil concluir por tanto que, con la ayuda del software, hemos obtenido una mejora en los tiempos de evacuación que de otro modo sería imposible determinar, a menos que se acometiera en la realidad la mejora constructiva.
Y el lector se preguntará, ¿cual es aquí el papel de la Estadística? Para no cansarle simplemente diré que los cálculos que realiza el software están basados en la probabilidad, que tiene cada persona a evacuar, de dar un paso en una dirección determinada, la distribución de tiempos (normales o uniformes) de paso, de reacción a una alarma, etc., y finalmente la distribución del tiempo total de evacuación de cada simulación. El valor puntual de tiempo que se concluye no es el tiempo medio sino el correspondiente al percentil 95, otro concepto estadístico que, quizá algunos de los lectores que hayan tenido hijos, conocerán por las tablas de pesos y estaturas que manejan los pediatras.